Proportional Relationships: A Simple Breakdown for Parents To Use at Home

As your child navigates middle school math, they'll encounter a foundational concept known as proportional relationships. It's a key building block in their understanding of mathematics, particularly when it comes to problem-solving and applying math in real-world situations. But what exactly is a proportional relationship, and how can you help your child grasp it? Don't worry – we've got you covered with this simple guide that breaks everything down in a way that's easy to follow.

At its core, a proportional relationship compares two quantities in a consistent way, such as the relationship between the number of hours worked and the total pay earned at a constant hourly rate. Proportional relationships help kids make sense of ratios and the real-life math they see all around them, from cooking recipes to calculating sales tax. Let's walk through the basics together and help your child build confidence in understanding proportional relationships.

What Are Proportional Relationships?

Proportional relationships compare two quantities, keeping the ratio between them the same regardless of how much those quantities change. 

Ratios are like a recipe for how two things relate: if you're baking and you need 2 cups of flour for every 1 cup of sugar, the ratio is 2:1. No matter how much more flour and sugar you use, the ratio stays the same as long as the relationship is proportional.

A key idea in understanding proportional relationships is the constant of proportionality. This term might sound complicated, but it just means the number that links the two quantities. For instance, if a car travels 60 miles in one hour, then the constant of proportionality is 60 – this is the constant speed. It's the number that tells you how one quantity (miles traveled) changes with another quantity (hours). 

You can see proportional relationships in other real-world situations, too, such as the amount of money you earn for hours worked or the number of gallons of gas used during a road trip.

How To Identify a Proportional Relationship

Helping your child identify proportional relationships starts with recognizing patterns. There are a few key ways to spot them, especially in middle school math problems:

• Tables. When you look at a table of values where two variables have a proportional relationship, you'll see that the ratio between the numbers in each row stays the same. For example, if 5 apples cost $10, then 10 apples will cost $20. The ratio of apples to dollars remains 1:2. This ratio should be consistent across the entire table.
• Graphs. In a graph of a proportional relationship, the plotted points will form a straight line that passes through the origin (0,0). This straight line tells us that, for example, as one variable increases, the other does too, at a constant rate. When your child works with ordered pairs on a coordinate plane, they can see how proportional relationships create clear, predictable patterns.
• Verbal descriptions. Word problems often describe proportional relationships. For example, if you read, "For every 3 cups of flour, you need 2 cups of sugar," that's a proportional relationship. The equivalent ratios (3:2) hold whether you're making a small batch or a large one. Help your child look for phrases like "for every" or "each" to recognize these relationships in word problems.

Key Proportional Relationship Concepts

To get a solid grasp on proportional relationships, there are a few important terms to understand:

• Unit rate. This is a simplified ratio where one of the terms is 1. For instance, if a car travels 240 miles in 4 hours, the unit rate is 60 miles per hour (240 ÷ 4 = 60). Unit rates are a great way to express a proportional relationship in its simplest form.
• Constant rate. In any proportional relationship, one quantity changes at a constant rate compared to the other. For example, if you're earning $15 per hour, no matter how many hours you work, you're always earning at the same rate – $15 for every hour worked.
• Rate of change. This tells us how quickly one quantity changes in relation to another. In a proportional relationship, the rate of change is always the same. For example, if your car uses 1 gallon of gas every 30 miles, the rate of change is 1 gallon per 30 miles.
• Independent and dependent variables. In a proportional relationship, the independent variable is the quantity you control (like the number of hours worked), and the dependent variable is the result that changes based on the independent variable (like the total money earned).

Understanding these concepts helps your child work through real-world situations like determining how much water is needed to fill a pool or how long it will take to complete a task based on constant speed.

Common Misconceptions and Mistakes

It's easy for students to mix up proportional relationships with other types of relationships, especially non-proportional relationships. Here are a few common pitfalls and how to avoid them:

• Confusing proportional and non-proportional relationships. A common mistake is assuming that all relationships are proportional. In a non-proportional relationship, the ratio between quantities isn't consistent. For example, if the cost of buying 3 apples is $3, but buying 6 apples costs $7, the ratio has changed. This is not a proportional relationship.
• Decimals and whole numbers. Some students might think that a ratio involving decimals isn't proportional. But proportional relationships can involve both whole numbers and decimals – as long as the ratio remains constant. For example, 1.5 hours for every 3 miles is a valid proportional relationship.
• Misinterpreting the graph. Sometimes, students expect all graphs to show proportional relationships as straight lines. However, a proportional relationship will always produce a straight line that passes through the origin (0,0). If the line doesn't pass through the origin, it's not proportional.

Helping your child avoid these misconceptions can give them a clear understanding of proportional relationships so they can confidently find the correct answers to mathematical problems.

Teaching Proportional Relationships at Home

Here are a few activities that you can do at home to make learning more fun:

• Use a number line. Plotting points on a number line can help your child see the relationship between two quantities. This is especially useful when comparing fractions and rational numbers.
• Scale drawings. Have your child create a scale drawing of their room or a favorite object. By using proportional relationships, they'll be able to create an accurate drawing based on different ratios.
• Benchmarking. Set small goals, or benchmarks, for your child to help them practice proportional reasoning. You could ask them to compare the amount of sugar in two different-sized drinks or calculate how many bricks are needed to cover a specific area in square feet.
• Lesson plans and activities. There are plenty of online resources that offer lesson plans focusing on proportional relationships. These can be interactive and engaging, making it easier for your child to grasp the concept.

By incorporating these activities into your child's learning routine, you'll help them strengthen their understanding of proportional relationships in a hands-on way.

Industry expert Jennifer Berce – a 5th-grade math teacher for more than 20 years – says, "When it comes to teaching your child about proportional relationships (or any mathematical content), be sure to make it relevant. Orchestrate discussions with your child while making connections to real-life situations."  

Using Proportional Reasoning for Real-World Problems

Proportional reasoning is a skill your child will use both in and outside of school. Whether they're calculating the simple interest on a savings account, figuring out a percent increase during a sale, or estimating how much sales tax they'll owe, proportional relationships play a big role.

Let's look at some everyday examples where proportional reasoning comes in handy:

• Percent problems. Your child might need to calculate what 15% off a $50 item is. They'll use proportional reasoning to determine that 15% of $50 is $7.50.
• Amount of water used. If your child is trying to figure out how much water it takes to fill a pool, they can use proportional reasoning. If it takes 100 gallons of water to fill ¼ of the pool, they'll know that it takes 400 gallons to fill the entire pool.
• Number of hours worked. When calculating earnings, your child can use proportional reasoning to determine how much they'll make based on the number of hours they've worked. For example, if they earn $10 per hour, they can multiply the number of hours worked by 10 to find their total pay.
• Total cost. Figuring out the total cost of multiple items based on price per unit is another example. If each pencil costs $0.50 and your child buys 8 pencils, they'll multiply 0.50 by 8 to get the total cost of $4.

These real-world problems offer a great way for students to see proportional reasoning in action and reinforce their understanding of proportional relationships.

Visualizing Proportional Relationships with Graphs

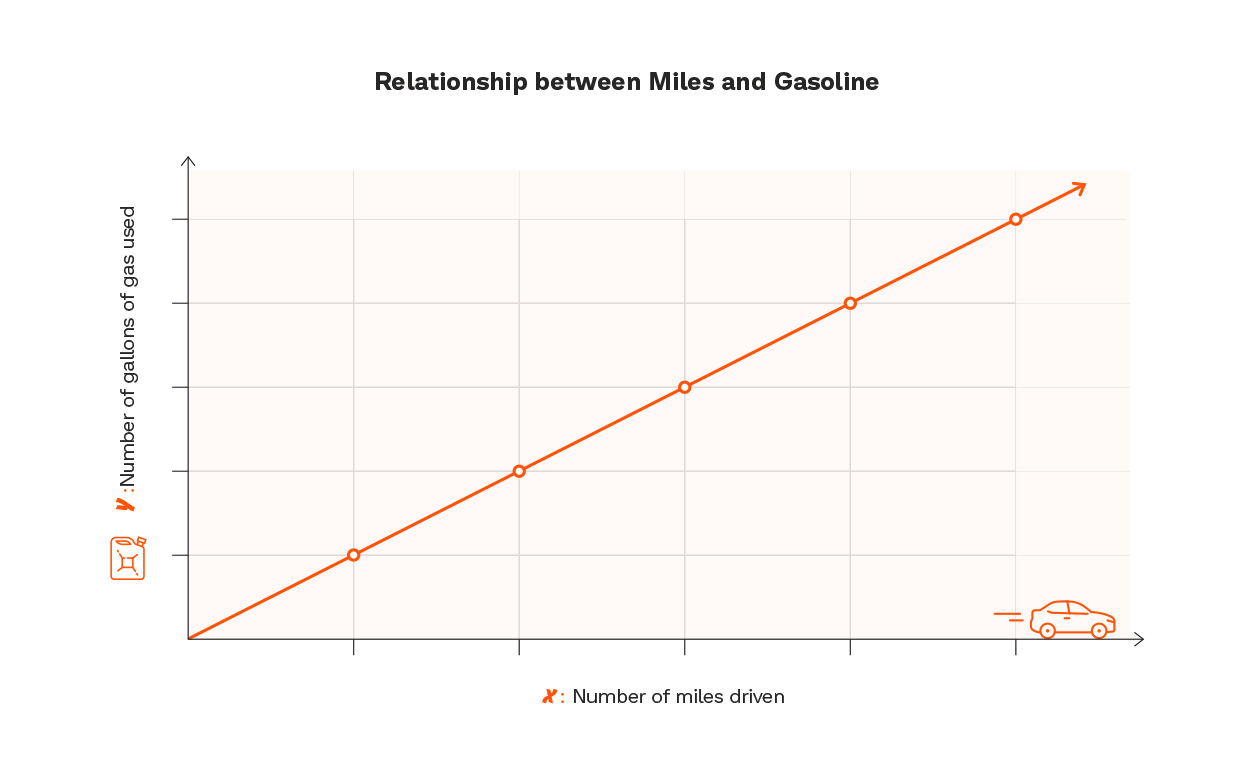
One of the most powerful tools for understanding proportional relationships is a graph. When your child plots points on a coordinate plane, they can see the relationship between variables come to life. In a proportional relationship, the graph will always show a straight line that passes through the origin.

For example, if your child is tracking the number of gallons of gas used on a trip compared to the number of miles driven, they can plot these values on the graph. If it's a proportional relationship, the line will be straight, showing that the amount of gas used increases at a constant rate as the miles increase.

The y-value represents one variable (like the number of gallons of gas used), while the x-value represents the other (the number of miles driven). Helping your child understand how a graph shows proportional relationships will deepen their understanding and give them a valuable skill they can use throughout their math journey.

Proportional Relationship Word Problems

Word problems are a great way to apply proportional reasoning in real-life situations. Help your child break down the problem step by step:

• Identify the ratios involved.
• Set up the proportional relationship.
• Use linear equations to find the unknown value.

For example, a word problem might ask: "If 4 books cost $20, how much would 7 books cost?" Your child can set up the proportional relationship (4/20 = 7/x) and solve for x, which is $35.

These types of problems are common in 7th-grade math and reinforce skills like simplifying ratios and calculating the quotient in proportional relationships.

Strengthening Students' Understanding of Proportional Relationships

Proportional relationships are a key part of your child's math education and a skill they'll use in everyday life. Practicing these concepts regularly and applying them to real-world situations can help your child develop a deep understanding of proportional reasoning. 

Encourage your child to solve word problems, plot points on graphs, and use ratios in their day-to-day tasks. With practice, they'll feel more confident in math and ready for the more complex topics they'll encounter in the future.

Looking for a fun, engaging way to help your child strengthen their math skills? Prodigy Education offers game-based learning that makes math exciting. With over 50 million students, parents, and teachers using our platform, Prodigy is designed to make learning math both fun and effective. Set goals, monitor progress, and watch your child build confidence in their math abilities. 

Learn more about Prodigy and how it can support your child's math journey today!